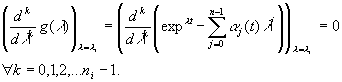Montrons que :

(1)

Le développement en série de Taylor de l'exponentielle conduit à :

(2)

Soit PA(l) le polynôme caractéristique de A, d'après le théorême de Cayley-Hamilton A est aussi racine de son polynôme caractéristique. On met en facteur PA(A) dans (2).

(3)

Pour le calcul des ak(t), on utilise le résultat suivant :

Si li est une valeur propre pour A alors f(li) est une valeur propre pour f(A). Notons :

d’après (3)

On obtient un système de n équations dont on tire les ak(t). Pour cette méthode il est nécessaire de connaitre les valeurs propres de A qui doivent toutes être distinctes. Si l_i est valeur propre multiple de A d’ordre n_i , il vient :